통계로 개념 이해하기
기술통계
- 데이터를 수학으로 기술하는 것
- 수치로 특징을 말하는 이유는 정확하기 때문
- 어떤 사실을 말할 때 높은 설득력
평균(mean)
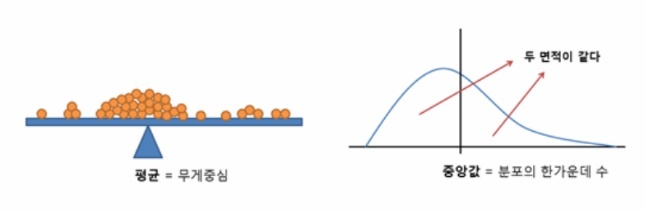
- 모든 데이터를 끌어안고 무게중심을 지키는 평균
기호( Summation)
의 정의는 다음과 같다.
- 모집답 vs 표본
- 모평균 vs 표본평균
- 모분산 vs 표본분산
- 모표준편차 vs 표본표준편차
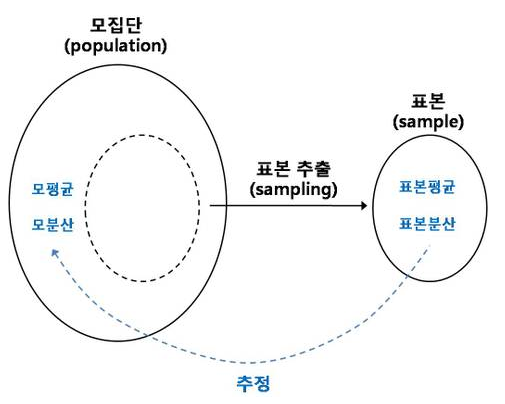
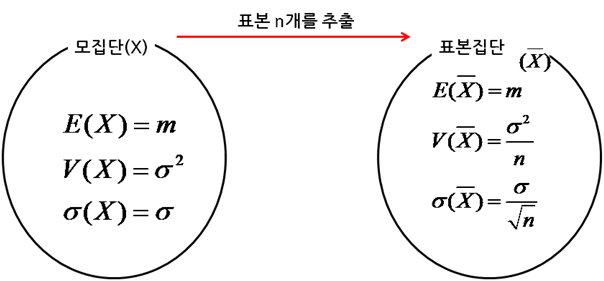
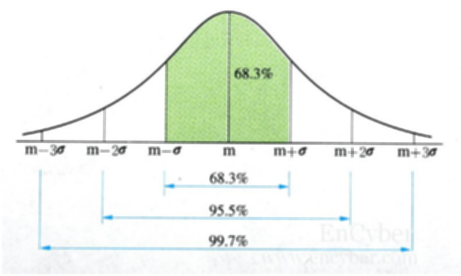
- 기술통계에서 말하는 값들은 모두 표본에 해당하는 값
아웃라이어(outlier)
- 평균을 크게 변하게 만드는 값
- 아웃라이어를 찾기 위한 그래프 Box Plot
- 무조건 제거 대상이 아니라 1차적 분석대상
- 왜 발생했는지와 데이터에 어떤 영향을 미치는 지등 파악
중앙값(median)
- outlier에 의해 데이터 대표값(평균등)이 많이 변하는 점 보완
- [52, 52, 60, 64, 76] 중앙값 60 (n+1)/2 의 위치 값
- [52, 52, 60, 62, 64, 76] 중앙값 61 n/2 와 (n+1)/2 의 평균값
범위
- 수치형 연속변수에서 최소값과 최대값 사이
- 범위는 특별한 의미를 가지는 경우가 별로 없음
- 아웃라이어등에 의해 범위가 커칠 수 있음 => 사분위범위 사용
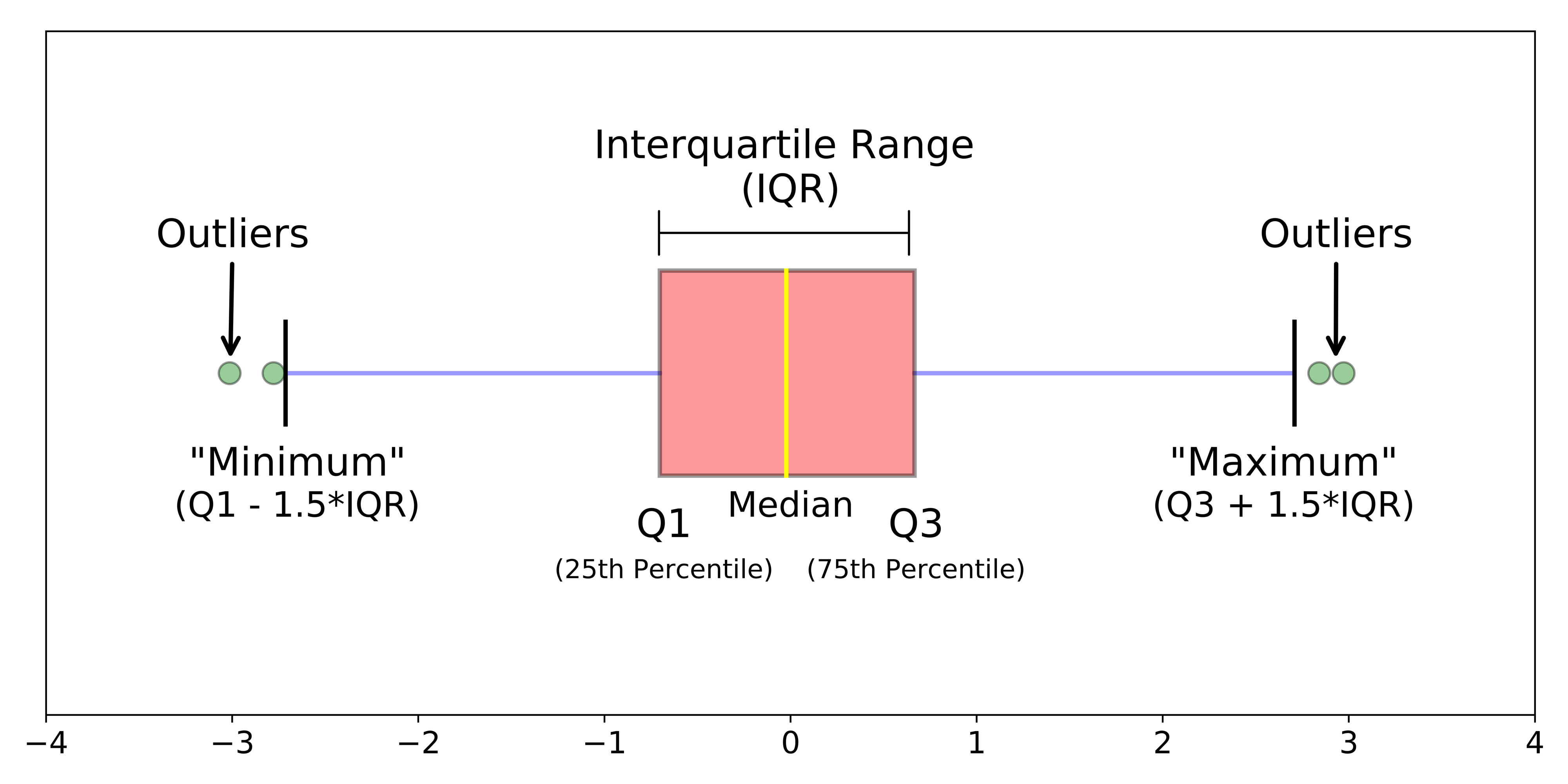
사분위범위(IQR, Interquartile Range)
- 데이터를 25%, 50%, 75%, 100%에서 25% ~ 75% 값
- 값은 중앙값으로 구함
- 중앙값 : 전체 데이터의 중앙에 있는 값 (≠ 평균)
- IQR : Q1(25%) ~ Q3(75%) 구간
산포도 - 얼마나 퍼져 있는가?
분산과 표준편차편차
- 자료값들이 특정값으로부터 떨어진 정도를 나타내는 수치
- 각 자료들이 평균으로부터 얼마나 떨어져있는지 그 거리(사실 '거리[거리는 양의 값만 가짐]'가 아니라 '차'입니다)를 보는 것
표준편차
- 통계량을 간단히 설정하기 위해 편차들의 대표값을 하나 설정
- 그 편차들의 대푯값을 설정하고 이를 표준(standard)로 이용
- 데이터들이 평균적으로 평균으로부터 떨어진 거리의 평균값
구하는 방법
- 각각의 자료값에서 특정값을 뺀 값의 절대값을 모두 더한 뒤 이의 평균을 구하는 방법 => 평균편차
- 각각의 자료값에서 특정값을 뺀 값의 제곱을 모두 더한 뒤 이의 평균을 구하는 방법 => 분산 => 표준편차
대푯값
- 대푯값은 편차를 최소로 만드는 값
- 평균편차 대푯값 => 중앙값
- 표준편차 대푯값 => 평균
산포도
- 자료값들이 대푯값으로부터 떨어진 정도
- 편차의 정의인 '자료값들이 특정값으로부터 떨어진 정도'에서 특정값 대신 대푯값을 넣으면 그것이 산포도
참고 편차들의 대표값으로 평균편차를 이용하지 않는 이유 편차란 각 자료들이 평균으로부터 얼마나 떨어져있는지 그 거리를 보기 위한 것 따라서 거리공식에 대입하여 자료값들이 평균값과 얼마나 떨어져있는지 평균적인 거리를 보아야 함 그래서 피타고라스 정리를 응용하여 만들어진 유클리드 거리(Euclidean distance)공식에 대입하여 평균낸 우리가 흔히 아는 표준편차 공식을 쓰는 것
표준화
'회귀' 할 때 중요함
- 각기 다른 집단의 평균과 표준편차를 비교하기 위해 평균을 0으로 이동시키고 표준편차로 나주어 준다
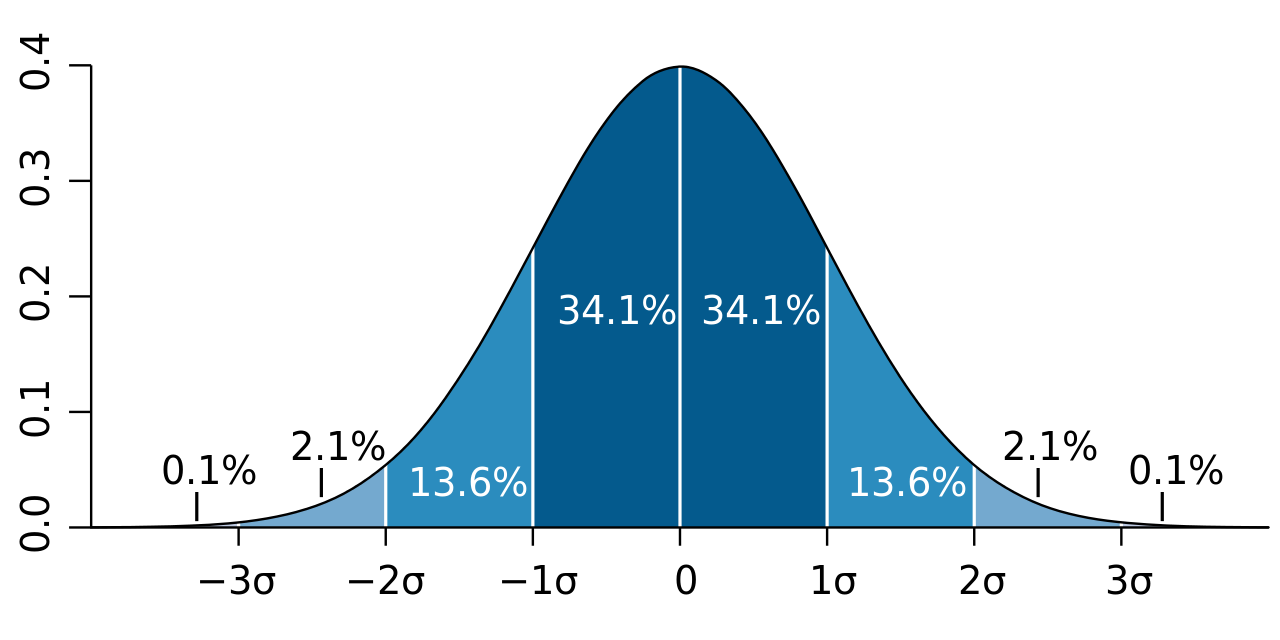
z-점수란 무엇일까요?
- z-점수는 자료가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 보여줍니다.
변동계수
- 평균과 표준편차가 다를 때 단수 얼마나 다른지 비율 만 확인
- 변동계수(V) = 표본표준편차(S) / 표본평규(x)
ex1)
- 몸무게 평균 63 / 표준편차 20 => 20 / 63 = 0.317
- 키 평균 175 / 표준편차 35 => 35 / 175 = 0.2
- 몸무게의 분포가 더 넗게 퍼져 있음
ex2)
- A기업 평균연봉 3500 / 표준편차 250 => 250 / 3500 = 0.0714
- B기업 평균연봉 4200 / 표준편차 180 => 180 / 4200 = 0.0428
- A기업의 연봉이 더 넓게 퍼져 있음('직급이 넓게 퍼져있구나' 정도를 예측할 수 있다)
공분산
- 변수가 2개일때 분산(공=함께)
- ex) 키와 몸무게의 분산을 같이 알고 싶을 때
- X가 커지면 Y도 커지거나 혹은 작아지거나 아니면 별 상관 없거나 등을 나타내어 주는 것
Cov(X,Y)
- Cov(X, Y) > 0 : X가 증가 할 때 Y도 증가
- Cov(X, Y) < 0 X가 증가 할 때 Y는 감소
- Cov(X, Y) = 0 공분산이 0이라면 두 변수간에는 아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계
- 두 변수가 독립적이라면 공분산은 0이 되지만, 공분산이 0이라고 해서 항상 독립적이라고 할 수 없다.
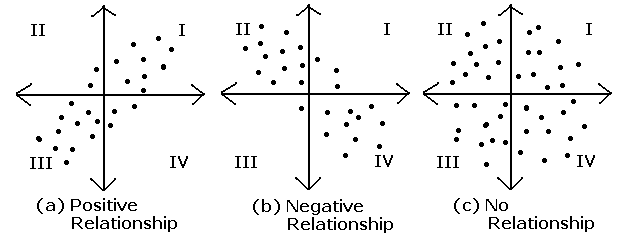
상관계수(Correlation)
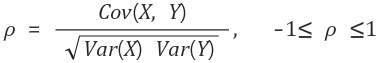
- 상관계수의 절대값은 1을 넘을 수 없다.
- 확률변수 X, Y가 독립이라면 상관계수는 0이다.
- X와 Y가 선형적 관계 -> 상관계수는 1 혹은 -1
- 양의 선형관계면 1, 음의 선형관계면 -1
독립 사건
- 사건 A가 사건 B에 영향을 주지 않는 상태(조건부 확률)
- 머신러닝에서 특정부분에서 조건부 확률이 많이 쓰인다.
- 따로 공부를 해야 할만큼 중요한 획을 이루는 조건부 확률
- cf) 베이지안 통계, 몬티홀문제 등 - 잘 설명해주는 유튜브 등이 있음
- 주사위 A 가 1 나올 때, 동전 B (앞면) 나올 확률?
배반 사건
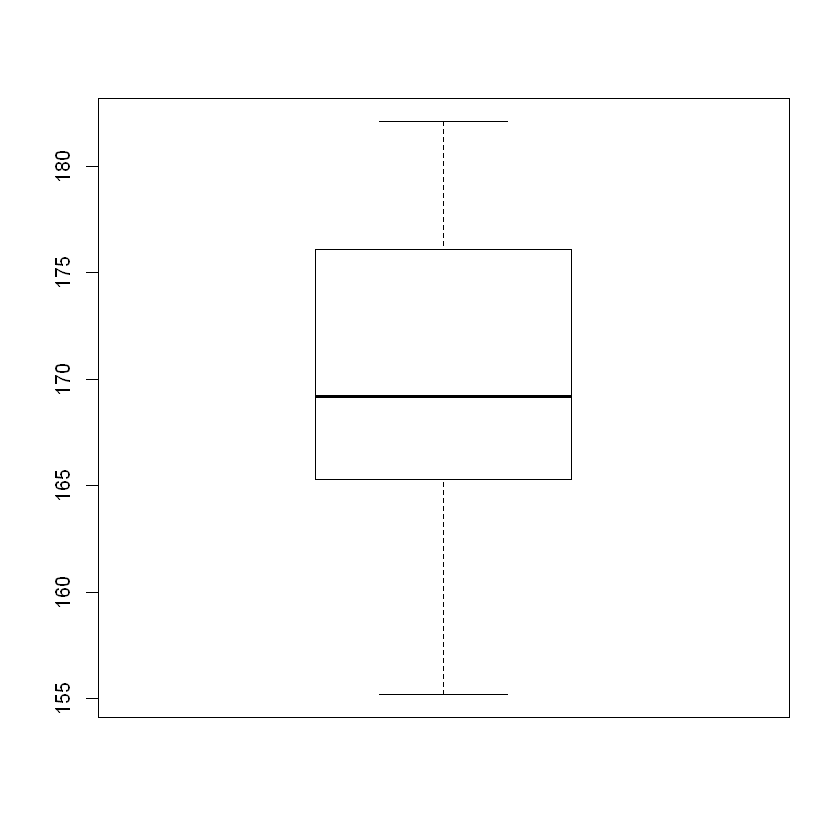
- 사건 A와 사건B가 동시에
- 동전을 던저 앞면(T)이 나오면 뒷면이 나올 수 없다
'독립사건이면서 배반사건인 경우' 를 생각해야 할 때가 있으므로 이 개념이 중요하다.
참고 | 양자역학
R로 기술 통계 구하기
In [8]:
# 데이터 로드
df <- read.csv('./rggagi/example_studentlist.csv')
In [9]:
head(df)
namesexagegradeabsencebloodtypeheightweight
| 김길동 | 남자 | 23 | 3 | 유 | O | 165.3 | 68.2 |
| 이미린 | 여자 | 22 | 2 | 무 | AB | 170.1 | 53.0 |
| 홍길동 | 남자 | 24 | 4 | 무 | B | 175.0 | 80.1 |
| 김철수 | 남자 | 23 | 3 | 무 | AB | 182.1 | 85.7 |
| 손세수 | 여자 | 20 | 1 | 유 | A | 168.0 | 49.5 |
| 박미희 | 여자 | 21 | 2 | 무 | O | 162.0 | 52.0 |
In [11]:
# 평균 구하기 - NA 제거 후
mean(df$height, na.rm = T)
170.035294117647
In [12]:
# 중앙갑 구하기
median(df$height, na.rm = T)
169.2
In [13]:
# 범위 구하기
range(df$height, na.rm = T)
- 155.2
- 182.1
In [14]:
# 사분위 구하기
quantile(df$height, na.rm = T)
0%155.225%165.350%169.275%176.1100%182.1
In [15]:
# IQR 구하기
IQR(df$height, na.rm = T)
10.8
In [16]:
# 참고 IRQ를 구하는 알고리즘은 여러개임
IQR(df$height, na.rm = T, type = 7) # default
IQR(df$height, na.rm = T, type = 5)
IQR(df$height, na.rm = T, type = 3)
10.8
11.775
13.9
In [17]:
# 평균, 중앙값, Q1, Q3 한번에 보기
summary(df$height, na.rm = T)
Min. 1st Qu. Median Mean 3rd Qu. Max.
155.2 165.3 169.2 170.0 176.1 182.1 In [18]:
# Box Plot 으로 보기 - NA 값 기본 제거함
boxplot(df$height)
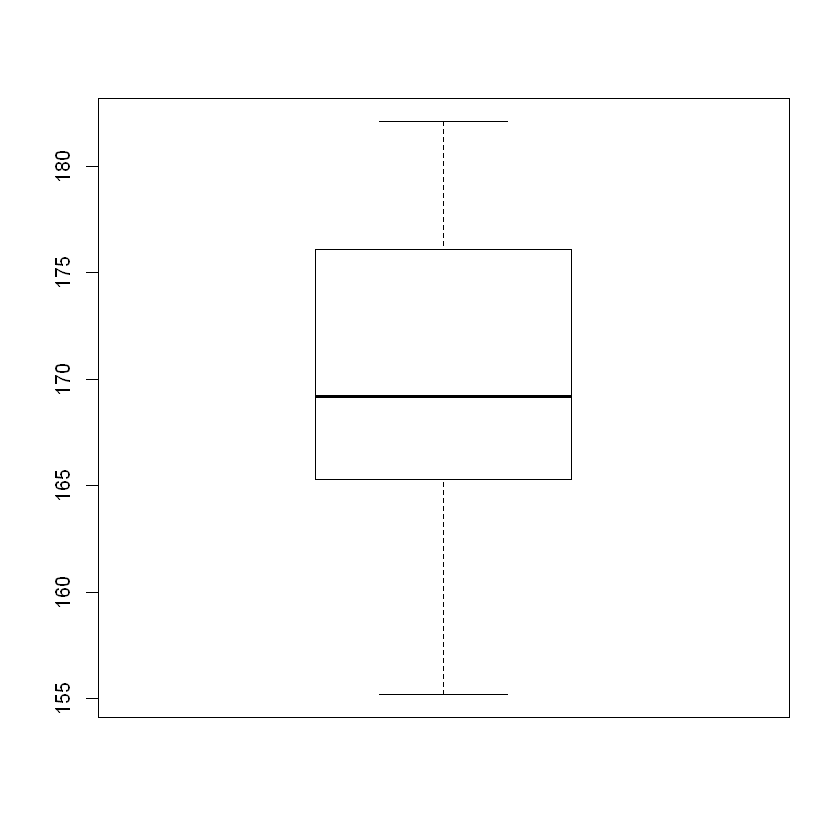
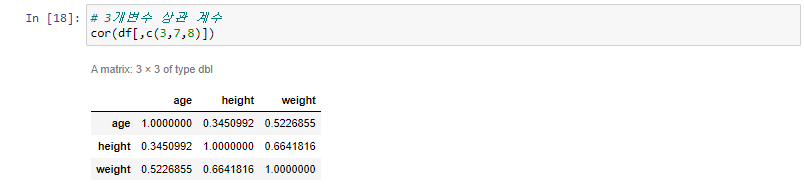
# 상관계수 다루기
cor(df$height, df$weight)
0.664181597958861
# 좀더 자세한 상관 관계
# 신뢰구간, P값등이 나옴
cor.test(df$height, df$weight)
Pearson's product-moment correlation
data: df$height and df$weight
t = 3.441, df = 15, p-value = 0.003639
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2696040 0.8677954
sample estimates:
cor
0.6641816

'프로그래밍 언어 > R' 카테고리의 다른 글
| r-ggagi-05-1 확률(Probability) (0) | 2022.10.14 |
|---|---|
| R-4.2.1 for Windows 다운로드 (0) | 2022.10.12 |
| R 기초 문법 (0) | 2022.10.12 |
